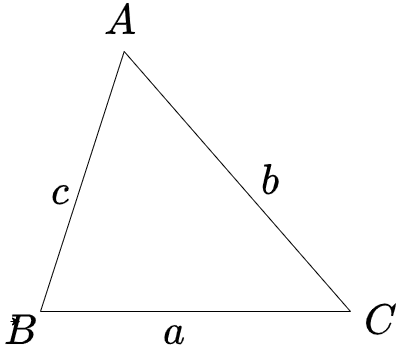
三角関数を用いた証明 ヘロンの公式は ① 三角関数 を使った面積公式 S = 1 2absinC ② 余弦定理 ③ 因数分解の公式 x2 − y2 = (x y)(x − y) の3つを使うと手早く証明することができますLINE 中学数学で学習する重要な公式たちをまとめておきます。 入試や学力テストなど 大きなテストの前には、こちらの記事で公式をチェックしておきましょう (^^) こちらのページで紹介している ヘロンの公式 三角形 ABC A B C の面積を S S とすると, s = ab c 2 s = a b c 2 として, S = √s(s −a)(s−b)(s −c) S = s ( s − a) ( s − b) ( s − c) 証明 三角形 ABC A B C に対し
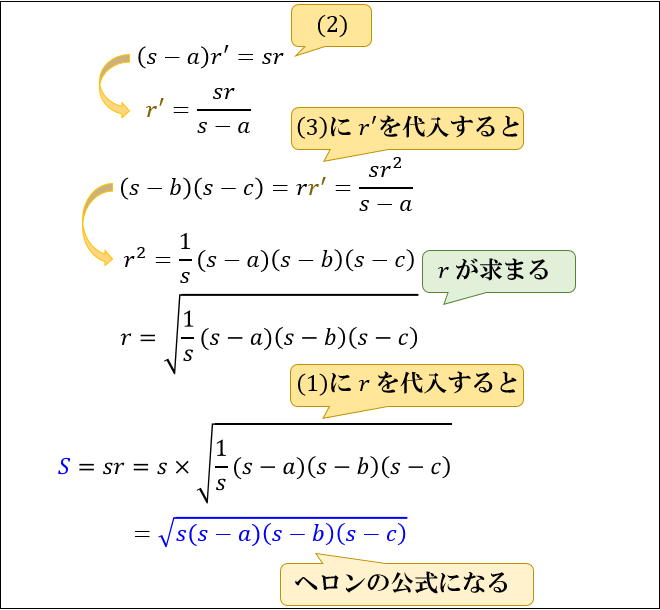
ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
ヘロンの公式 証明 中学数学
ヘロンの公式 証明 中学数学-16 hours ago ゆっくり数学解説平面図形(「ヘロンの公式の証明」後編) 解説・講座 今回も前回に続き、ヘロンの公式の証明を扱います。 また、初めて入試問題解説にも挑戦しました。中学数学公式一覧 Ver112 (21 年5 月6 日作成) 1 計算の公式 11 交換法則・結合法則・分配法則 加法の交換法則 ab = ba 加法の結合法則 abc = (ab)c = a(bc) 乗法の交換法則 ab = ba 乗
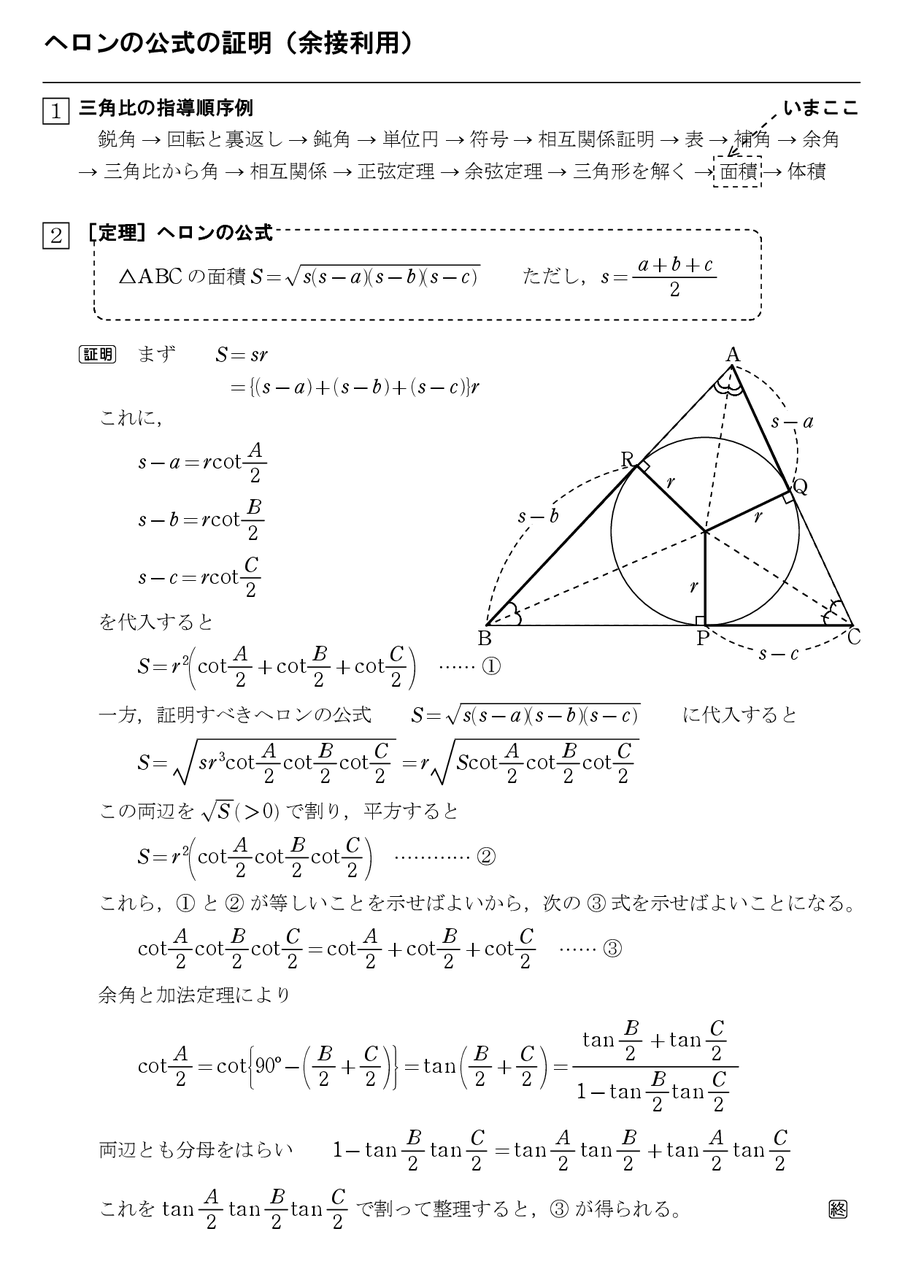



ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する
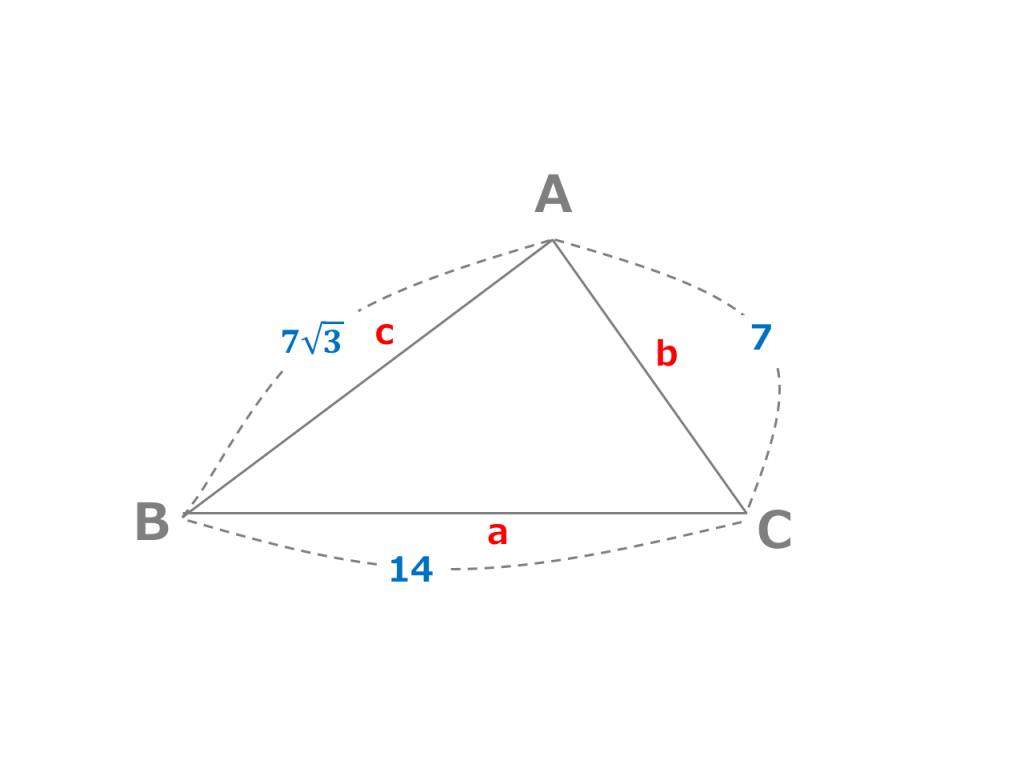
ヘロンの公式で求めた面積は、他の方法で求めた面積と等しいはずだということを使います。 例 三角形の3辺の長さが,それぞれ13,14,15のとき,内接円の半径を求めなさい (答案) ヘロンの公式は、三角形の3辺の長さから面積を求めるための公式です。 なぜ3辺の長さから面積が求められるのでしょうか? そもそも三角形の面積は「底辺 × 高さ ÷ 2」なので、高さデジタル大辞泉 ヘロンの公式の用語解説 三角形の面積Sを3辺の長さa・b・cから求める公式。3辺の和の半分をsとすると、S2=s(s-a)(s-b)(s-c)で与えられる。古代ギリシャの数学者
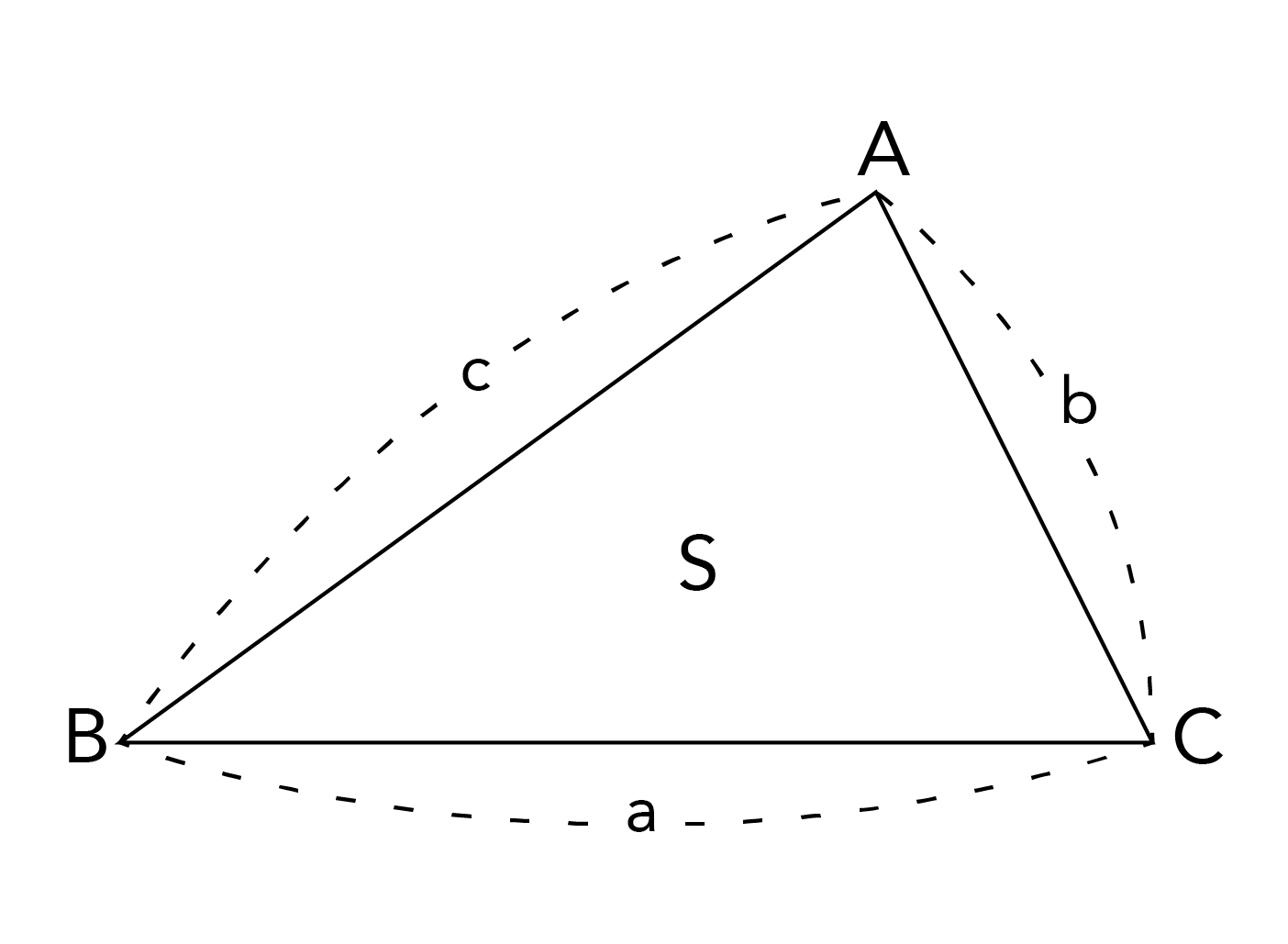
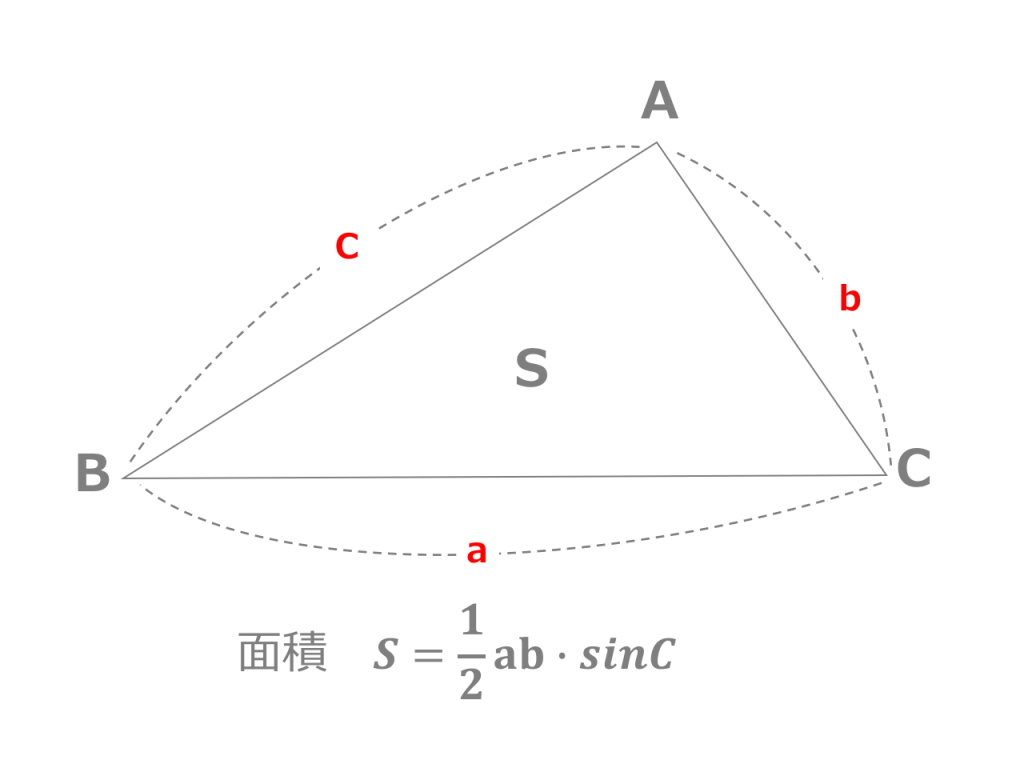
ヘロンの公式の補足 最後に補足を2点紹介しますね。 補足1:違う面積の式を使っても同様に証明ができる 今回は、 S = 1 2 a b sin C で証明しましたが、他の式を使っても証明できます 証明 ヘロンの公式 ヘロンの公式を証明します。 まず三角形ABCを考えます。 角 ( A, B, C ) に向かい合う辺をそれぞれ ( a, b, c ) とします。 ここで三角形の面積が ( frac {1} {2} bc sinヘロンの公式(幾何的証明) 三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 と表せる。 以下の説明では、左図のように、頂点および角度をA,B,Cで表し 各頂点に向かい合う
ヘロンの公式とその証明(数1) 000 1259 ヘロンの公式とその証明(数1) 5,662 views 98 Dislike Share Save 数学を数楽に 7K subscribers 3辺の長さが分かってるとき ヘロンの公式の拡張(プラーグマグプタの公式) 円に内接する4角形の4辺を、 としたときの、内接4角形の面積 を求める公式です。 プラーグマグプタは、7世紀のインドの数学者でヘロンの公式(ヘロンのこうしき、英 Heron's formula)とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。 公式 証明 三角関数を用いた証明 ピタゴラスの
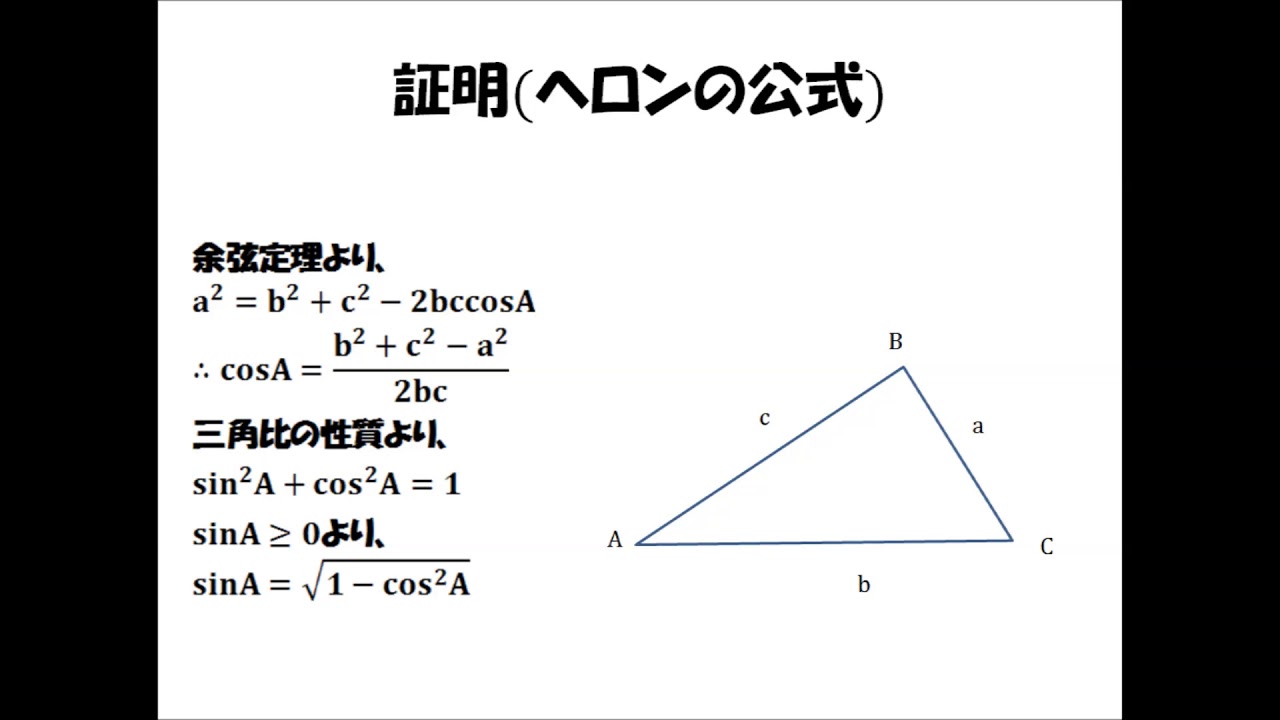



Haruka先生の数学証明シリーズ ヘロンの公式 Youtube



あなたの好きな数学の定理や公式はなんですか またそれはなぜですか Quora
3 3 辺の長さ a, a, b, b, c c と面積 S S が整数であるような三角形を ヘロンの三角形 (Heronian triangle)と呼ぶ また, ヘロンの三角形の 3 3 辺の長さの組 (a,b,c) (a,b,c) を ヘロン数 (Heronianヘロンの公式 (ヘロンのこうしき、 英 Heron's formula )とは、3辺の長さが a, b, c などと分かっている 三角形 の 面積 S を求める 公式 のことである。 アレクサンドリアのヘロン が彼の著書『 今回は 「ヘロンの公式」 について 解説しました! 簡単な公式ですが 知ってると知らないとでは 大違いなのできっちりと 覚えて現場で使ってみてくださいね♪ また今回から数回は




ヘロンの公式の証明方法を解説 三角形の面積の公式から導く方法 トムラボ




ヘロンの公式を証明する トムラボ
ヘロンの公式(代数的証明) 幾何的証明はこちら 三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 と表せる。 以下の説明では、左図のように、頂点および角度をA,B,Cで表ヘロンの公式を三平方の定理から導く 3辺の長さがa,b,cであるような ABCの面積Sは、2t=abcとおくと、次式で求まる。 となる。 証明1三角関数を使うものがよく知られている。 証明2三平 ヘロンの公式三角形の面積 大学入試数学の考え方と解法 大学入試で出題される数学の問題を解くときの着眼点・考え方・解法の糸口の掴み方を伝えます。 理解とかどうでも良い




ヘロンの公式の証明 導出 を徹底解説 5分でわかる Youtube




中学数学で出来る ヘロンの公式の証明
証明や四角形版もわかりやすく解説! 22年1月18日 この記事では、「ヘロンの公式」やその証明についてわかりやすく解説していきます。 また、ヘロンの公式の四角形バージョンピックの定理に戻る 卒業研究 TOP ヘロンの公式 三角形の面積を求めるときに用いたヘロンの公式を紹介します。 <証明> 使用する公式 ・三角関数の基本公式 sin 2 Acos 2 A=1 ・余弦定理 a 2 =bヘロンの公式の証明 では、なぜこのような公式で面積を求めることができるのか。 その証明方法について確認しておきましょう。 証明はちょっと複雑な式変形を伴います。 オレは公式が使えたらそ



Q Tbn And9gcqsmhzhqafatw3pgwcoqpy C1 Vvq11yg5vjwxgrwlnhinvbprxyypi Usqp Cau




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
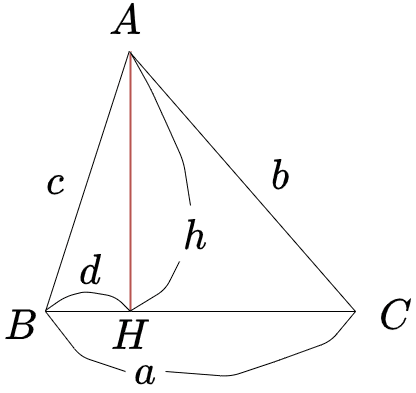
ヘロンの公式の証明 三角比相互の関係 (平方関係)より sin 2 θ + cos 2 θ = 1 (1) 公式(1)を変形して、因数分解すると sin 2 A + cos 2 A = 1 sin 2 A = 1 - cos 2 A = ( 1+ cos A ) ( このとき、三平方の定理から c = bd ad = √ (a^2 h^2) √ (b^2 h^2) となるので、これを h について解きます (a^2 h^2) 2√ (a^2 h^2) √ (b^2 h^2) (b^2 h^2) = c^2 ⇒ 4中学レベルで分かる! ヘロンの公式の証明 1,244 views 3 Dislike Share Save PjxeWEv 16 subscribers ヘロンの公式の証明です。 中学までの数学の知識で証明しました。 必要に応じて一
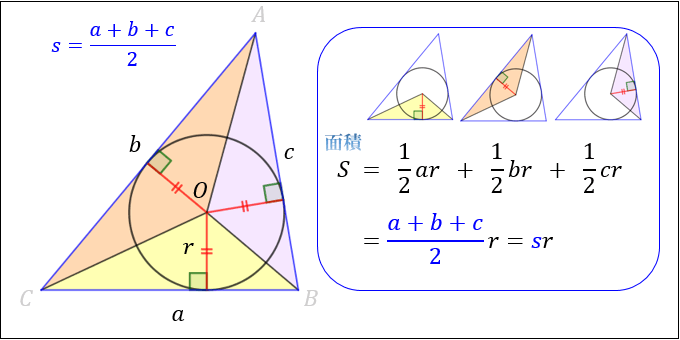



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



Q Tbn And9gcqoo Brlxk8uvd0nozzdddei7hxbvlcypnvdn C193zdzbwjeuwbhgl Usqp Cau
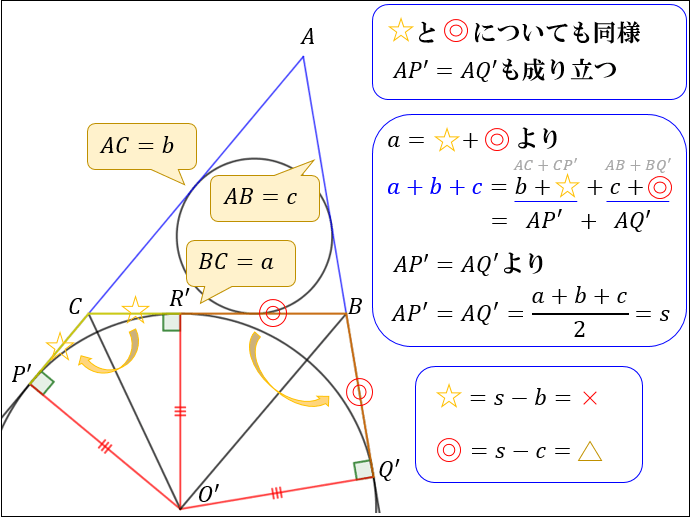
ヘロンの公式の証明には、 内接円の性質を利用した証明と三角関数を用いた証明 があります。 証明は少しむずかしいですが、証明方法を知ることでより理解が深まり、他の問題を解くそこで今回は中学生の数学の公式を一覧で紹介します。図形の定理から解の公式まで、中1・中2・中3で習う公式を網羅的にまとめたので参考にしてください。 証明問題 図形の証明問題は中学生三角形の3辺の長さで面積を表す,次の公式を「ヘロンの公式」という (ヘロン:ギリシャの測量家,1世紀頃) ABC の三辺の長さを a, b, c とし, とおくと, ABC の面積 S は,次の式で表され




ヘロンの公式 Wikipedia




Haruka先生の数学証明シリーズ ヘロンの公式 中学レベル Youtube
ヘロンの公式 高精度計算サイト ヘロンの公式 ホーム / 私の自作式 / サンプル 三角形の面積をヘロンの公式から求めます。 辺 a 辺 b 辺 c 面積 S お客様の声 アンケート投稿 よくある質 navy engineer 二重根号 公式 数学 証明 高校数学 "二重根号"の公式とその証明 です! 目次 二重根号 公式 証明 問題 目次 1 ヘロンの公式を解説します! 2 ヘロンの公式とは 3 ヘロンの公式の証明 31 三角形の面積は「底辺×高さ÷2」で求められる 32 三角形の高さは「斜辺×sinθ」で求められる




ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




壁掛けミラー ウッディ モダン 木彫りミラー シード W500 H10 ホワイト Ab 23w 天然木 木枠 デザイン バリ島 玄関 店舗 高級品
ヘロンの公式 三角形の面積を求める公式に ヘロンの公式 というものがあります。 これまで 底辺×高さ÷2 サインを使って三角形の面積を求める公式 内接円をもつ三角形の面積を求める公式 と三角ヘロンの公式公式ヘロンの公式 3辺の長さがそれぞれ, , であるような三角形の面積は次の式で求まる但し, とする ヘロンの公式は, 三角形の3辺の長さが分かっているときにその面積を求めるための ヘロンの公式 とは, 三角形の 3 3 辺の長さを用いて面積を計算する公式 です.具体的には次の式で表されます. ヘロンの公式: ABC A B C の三辺の長さを a,b,c a, b, c とする. s =




Rsdo9i Ud4lsjm




ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する
ヘロンの公式 を証明します。 三角比の相互関係 より、 sin 2 C cos 2 C = 1 を使うと面積の公式を以下のように変形することができる。 sin C = 1 − cos 2 C より、 S = 1 2 a b sin C




中学生版 ヘロンの公式 三平方の定理が楽に計算できる方法 Youtube




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



ピタゴラスの定理の証明方法は何でしょうか Quora




ヘロンの公式 Twitter Search Twitter




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典




ヘロンの公式の導き方ヘ 中学生向け てっぃちmarshの数学 Mathematics 教室



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典




Haruka先生の数学証明シリーズ ヘロンの公式 中学レベル Youtube



数学のヘロンの公式って中学高校で習った記憶ないんですけど 三角関数で Yahoo 知恵袋



中学数学で出来る ヘロンの公式の証明




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




ヘロンの公式 Twitter Search Twitter




三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




数学三角形と比の人気動画を探索しましょう Tiktok




高校数学 三角形の面積のヘロンの公式s S S A S B S C の証明と利用 受験の月




3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ




ヘロンの公式を証明する トムラボ




ヘロンの公式 Wikipedia



アンダーアーマー Ua Jet 21 Syn メンズ レディース バスケットボール シューズ バッシュ D ブラック ホワイト Under Armour Sale 67 Off



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ




ヘロンの公式 その証明 身勝手な主張



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ




ヘロンの公式 Wikipedia




中学生版 ヘロンの公式 三平方の定理が楽に計算できる方法 Youtube



中学数学で出来る ヘロンの公式の証明




三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する
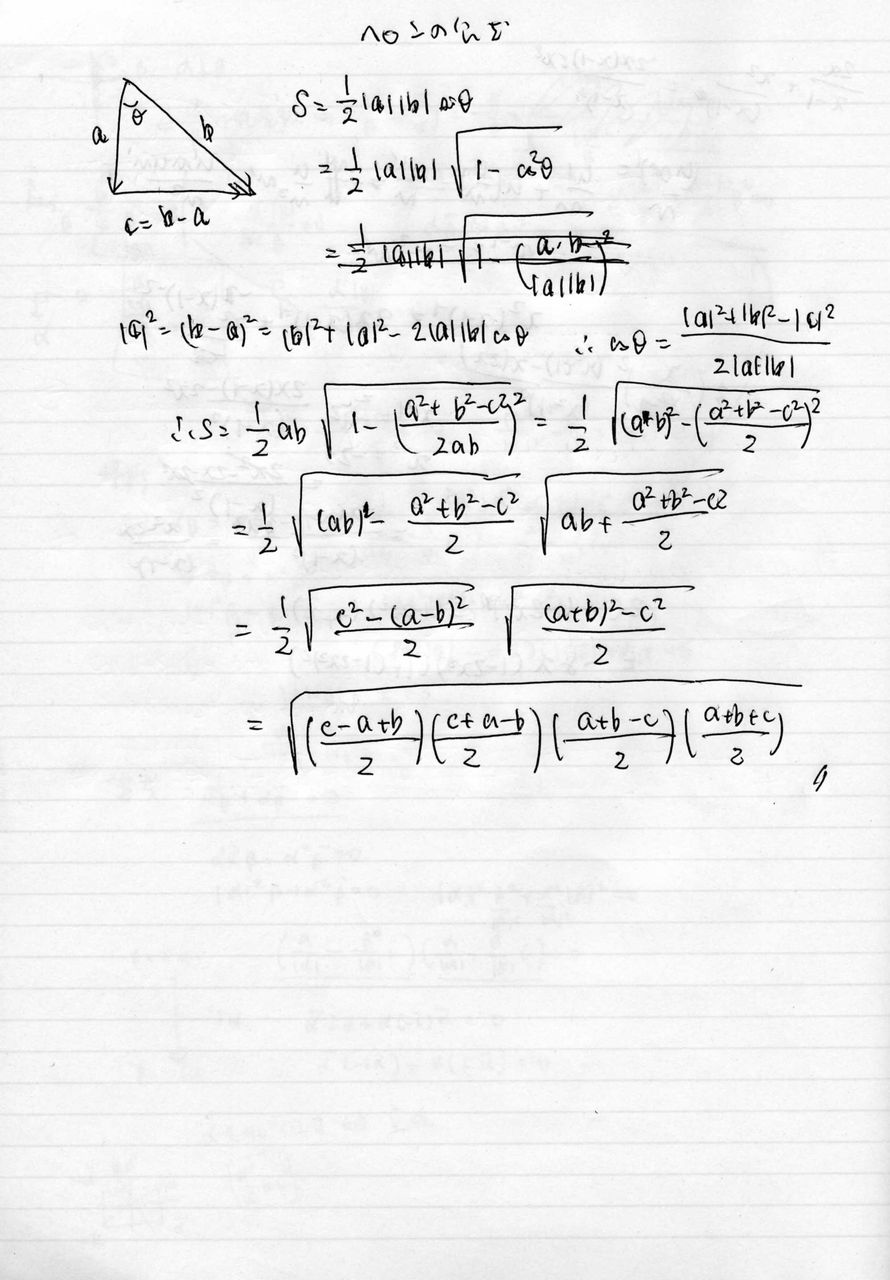



ヘロンの公式 東大合格コム



この数学の問題を ヘロンの公式を使わずに 三平方の定理での解き方を教え Yahoo 知恵袋




3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ



ピタゴラスの定理の証明方法は何でしょうか Quora




ヘロンの公式の証明と例題 数学i By ふぇるまー マナペディア



中学数学で出来る ヘロンの公式の証明




3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ
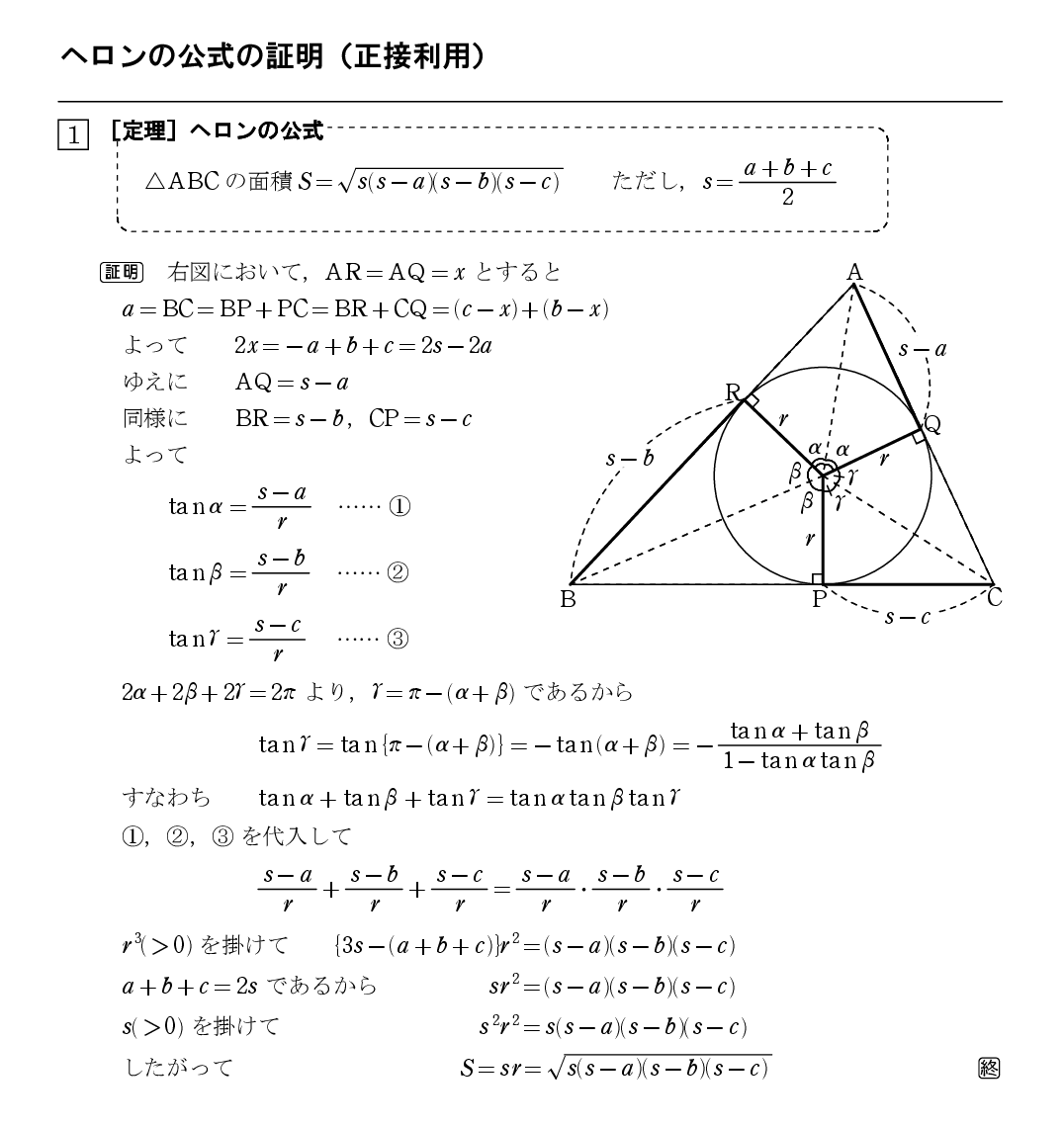



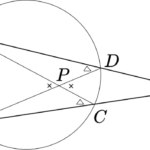
授業での雑談ネタ 18 ヘロンの公式の有名でない証明 怜悧玲瓏 高校数学を天空から俯瞰する
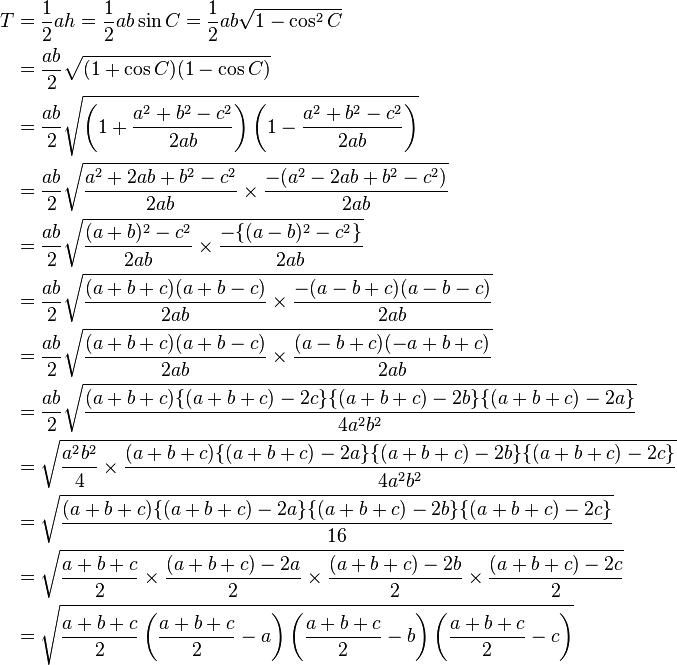



ヘロンの公式の証明 三角関数を使わずに ようこそ なるのホームページへ



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




Haruka先生の数学証明シリーズ ヘロンの公式 Youtube



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




数学三角形と比の人気動画を探索しましょう Tiktok




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典



ヘロンの公式の部屋



数学のヘロンの公式って中学高校で習った記憶ないんですけど 三角関数で Yahoo 知恵袋



中学数学で出来る ヘロンの公式の証明




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri




3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri




ヘロンの公式 Wikiwand




中学数学で出来る ヘロンの公式の証明



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典




ヘロンの公式 導出と計算例




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri




ヘロンの公式 東大合格コム
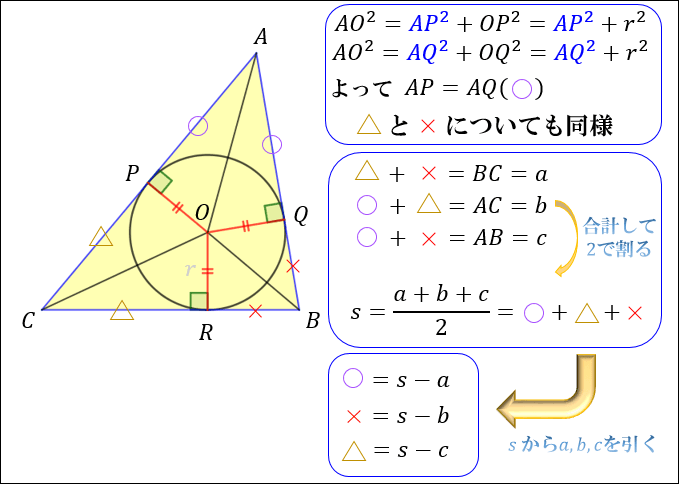



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



Q Tbn And9gcqizwnyd0yvcyqaubg5ss3g42oga805ssp7azdsubyurduciomulcsg Usqp Cau



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典




中学生版 ヘロンの公式 三平方の定理が楽に計算できる方法 Youtube
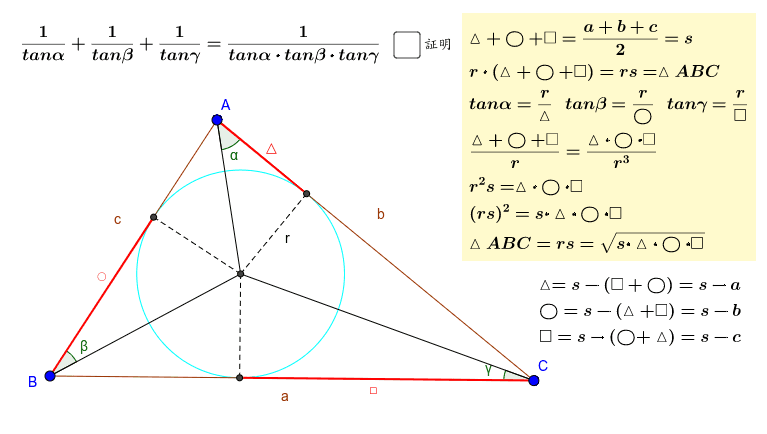



ヘロンの公式 Geogebra




ヘロンの公式の証明と使用例 高校数学の美しい物語



ヘロンの公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開
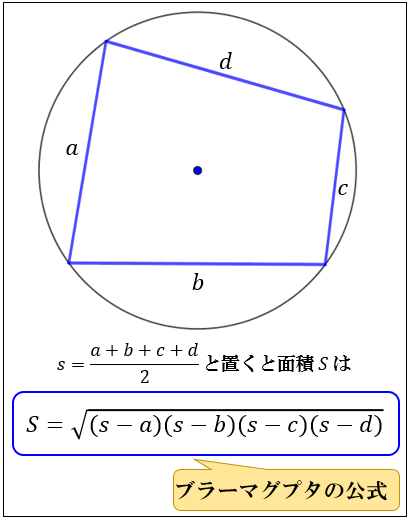



日暮里くん Al Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式 T Co Ir01crbs61 Twitter
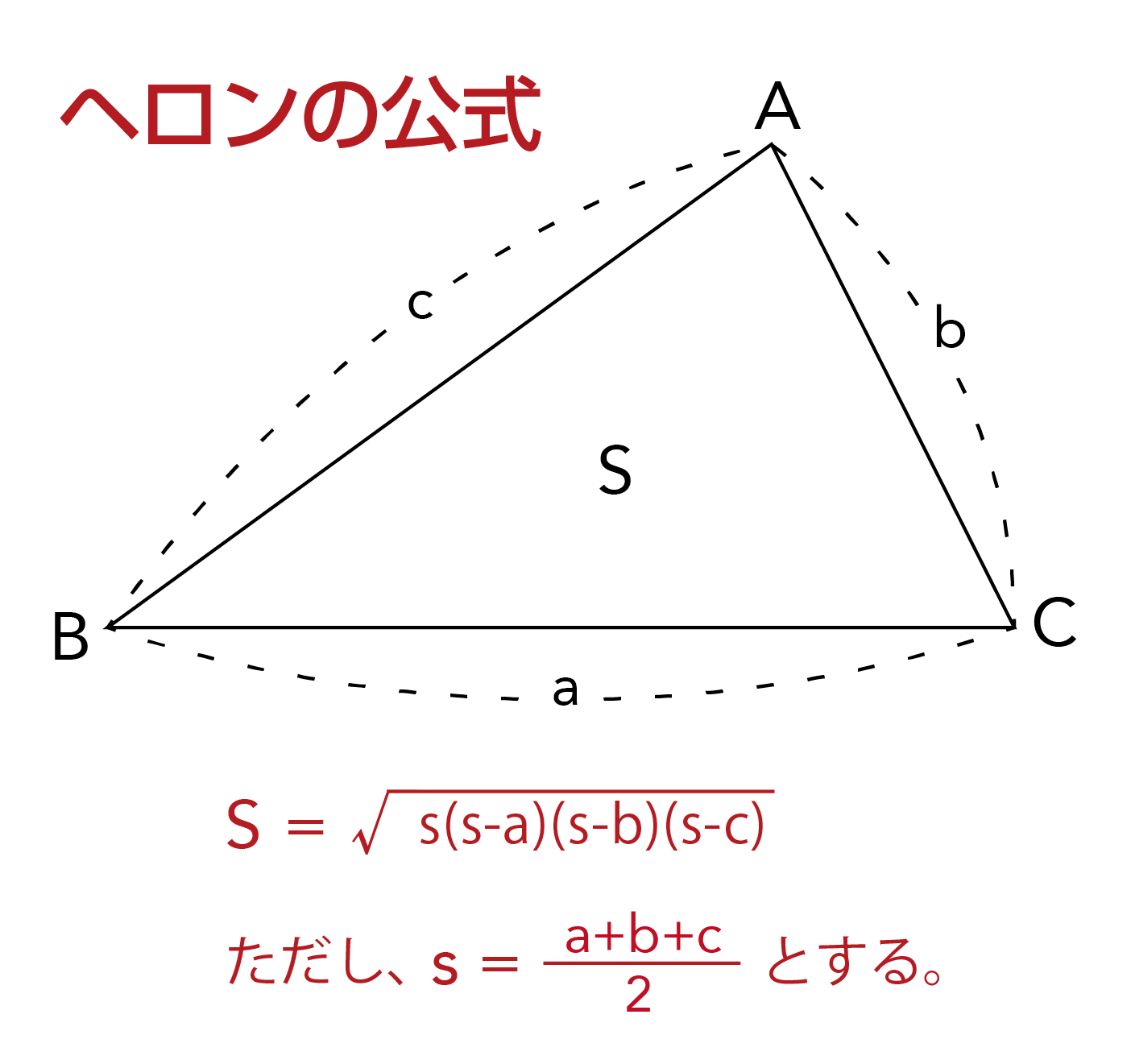



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




中学生版 ヘロンの公式 三平方の定理が楽に計算できる方法 Youtube




ヘロンの公式の証明と例題 数学i By ふぇるまー マナペディア



Q Tbn And9gcrjablmqqdnbh6nrccoynqcph8aet1e Anabpoq3hsqjwzgrkooy0pl Usqp Cau




ヘロンの公式のスモールsってどういう意味でしょうか 誰か教えてくださいm M 基塾長の成績の上がるブログ




中学数学で出来る ヘロンの公式の証明




ヘロンの公式のスモールsってどういう意味でしょうか 誰か教えてくださいm M 基塾長の成績の上がるブログ



ヘロンの公式についてs A B C 2s S S A Yahoo 知恵袋
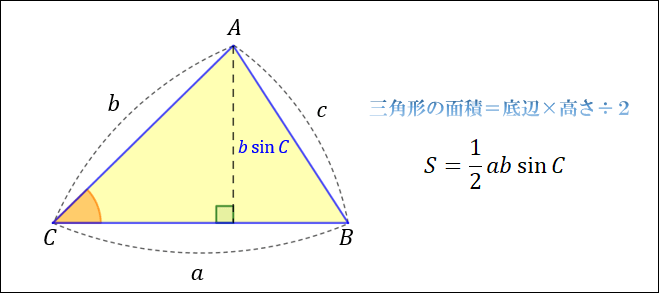



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
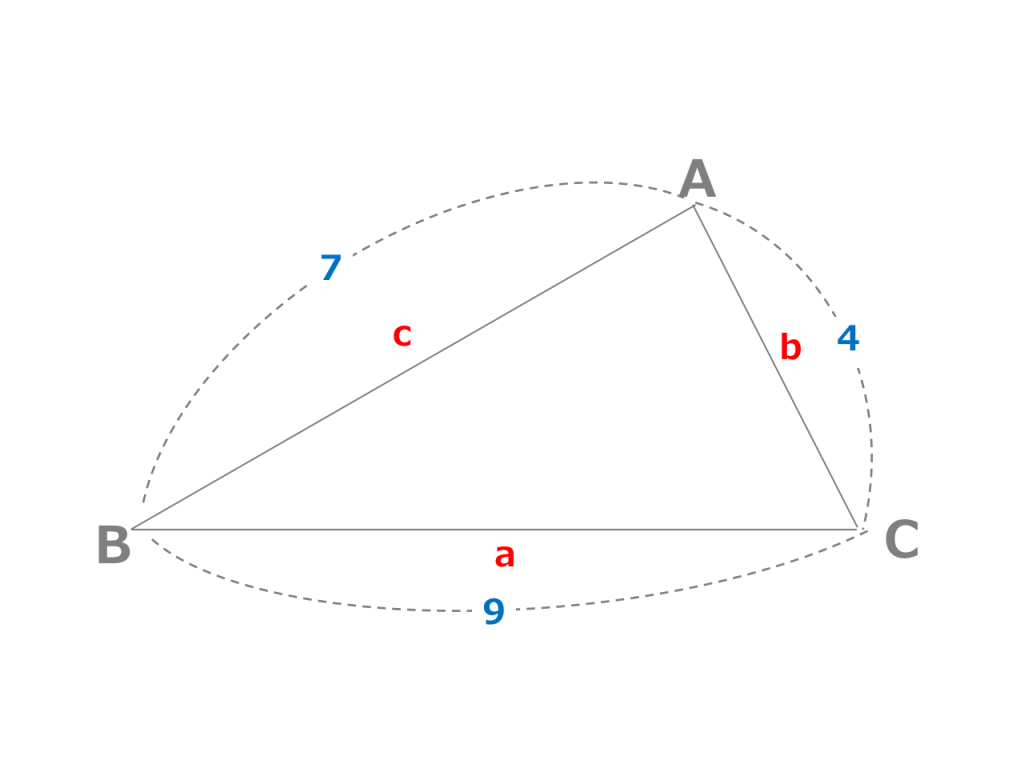



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ
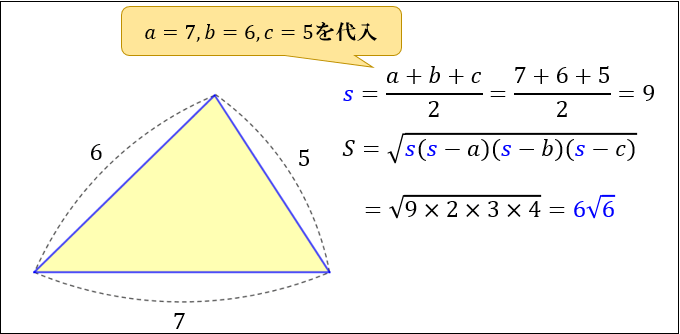



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典



ヘロンの公式の部屋




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



ヘロンの公式とは 証明や四角形版もわかりやすく解説 受験辞典
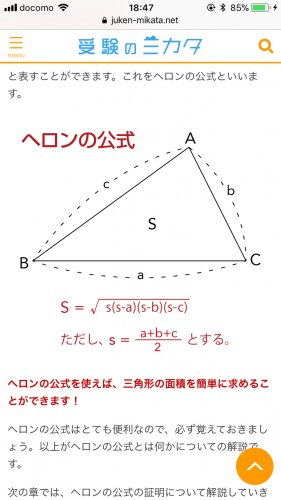



ヘロンの公式なんですが Sって面積のことですよね なのにs 2分のa B 高校受験 教えて Goo




三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する



この数学の問題を ヘロンの公式を使わずに 三平方の定理での解き方を教え Yahoo 知恵袋




ヘロンの公式 計算を工夫して証明 今週の定理 公式no 4 Youtube
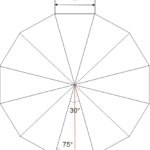



中学数学で出来る ヘロンの公式の証明




Haruka先生の数学証明シリーズ ヘロンの公式 中学レベル Youtube



0 件のコメント:
コメントを投稿