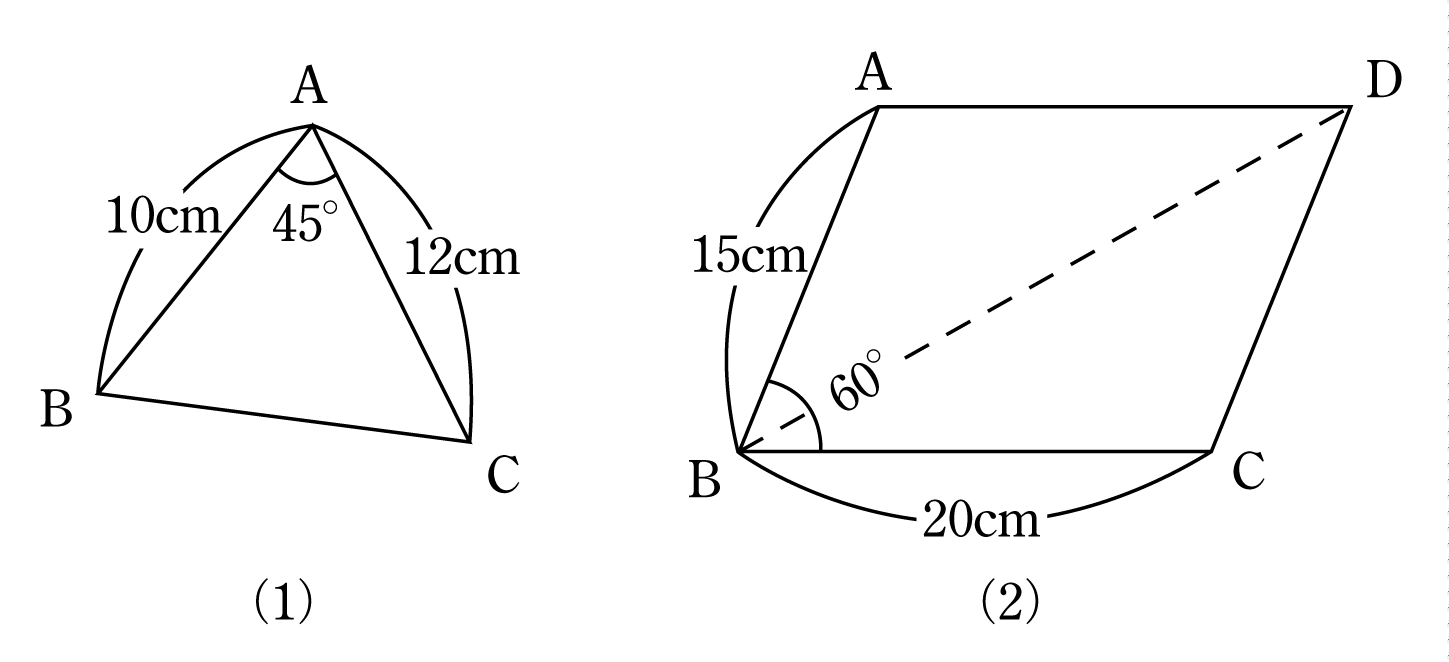
Abcdの対角線の交点oを通る直線が 辺ad tbcと交わる点をそれぞれ m t nとする このとき mo=noであることを証明 しなさい z証明 { aomと conにおいて 平行線の錯角は等しいからad//bcより ∠mao=∠nco・・・① 平行四辺形の対角線はそれぞれの中点で交わるから 2) 平行四辺形の対角線の交点をO、各頂点をABCDとする。 かなり省略して証明するが、∠AOB=∠BOC=∠COD=∠DOA=90° 平行四辺形の対角線はそれぞれの中点で交わる。 よって、対角線で区切られた4つの三角形は全て合同。 故に、4つの三角形全ての斜辺は等しい。平行四辺形の対角線 □ABCDはAB=10cm, BC=9cmである。 DからBCの延長線上に引いた垂線の長さが8cmのとき
Http Www News Ed Jp Gimu Yumeako Gakuryoku H26 H26cyusu H26cyusua 7 Pdf
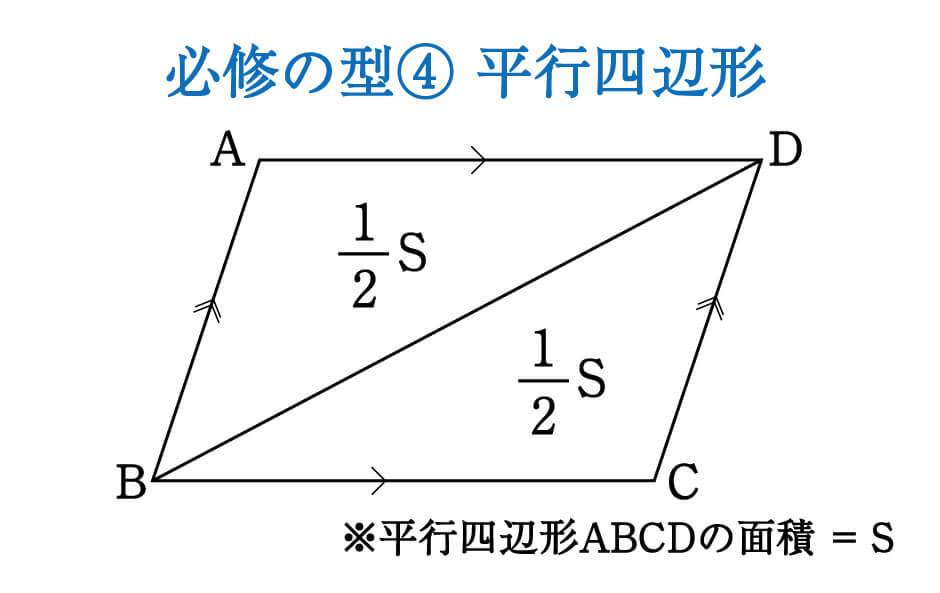
平行四辺形の対角線
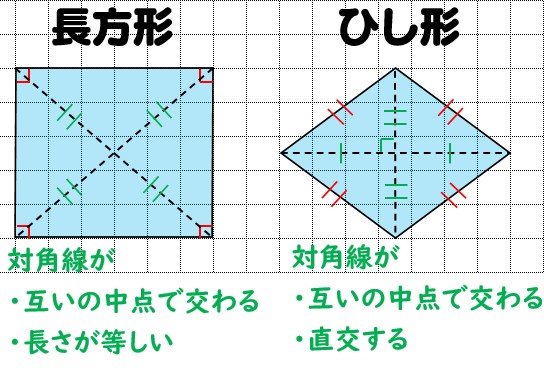
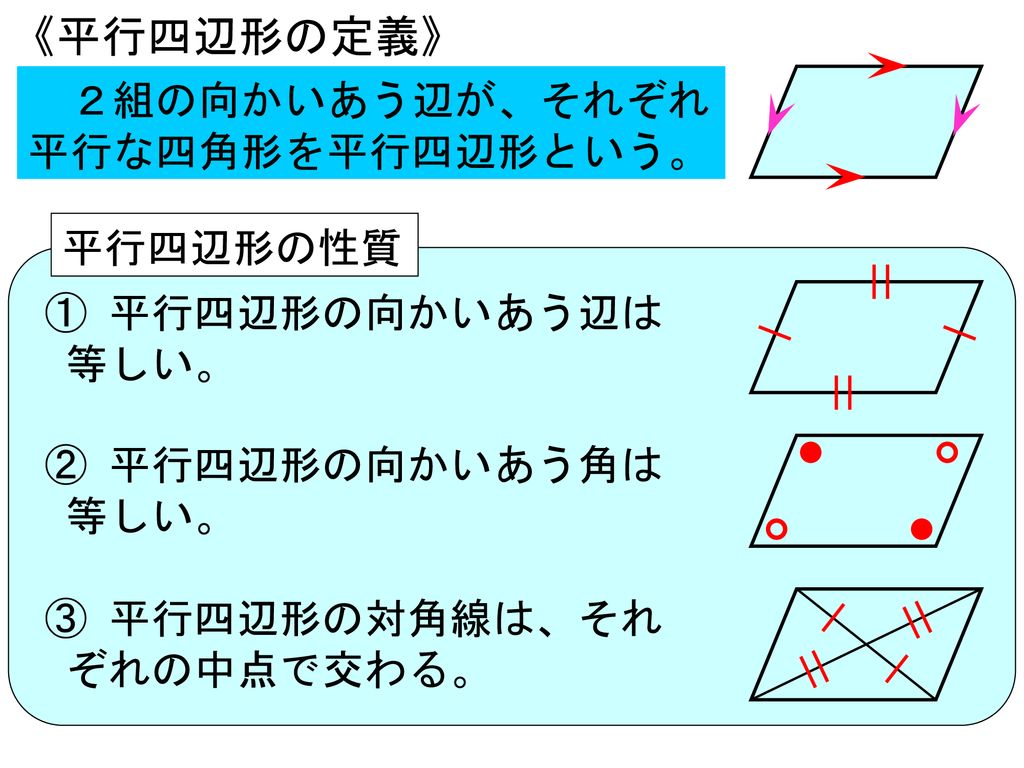
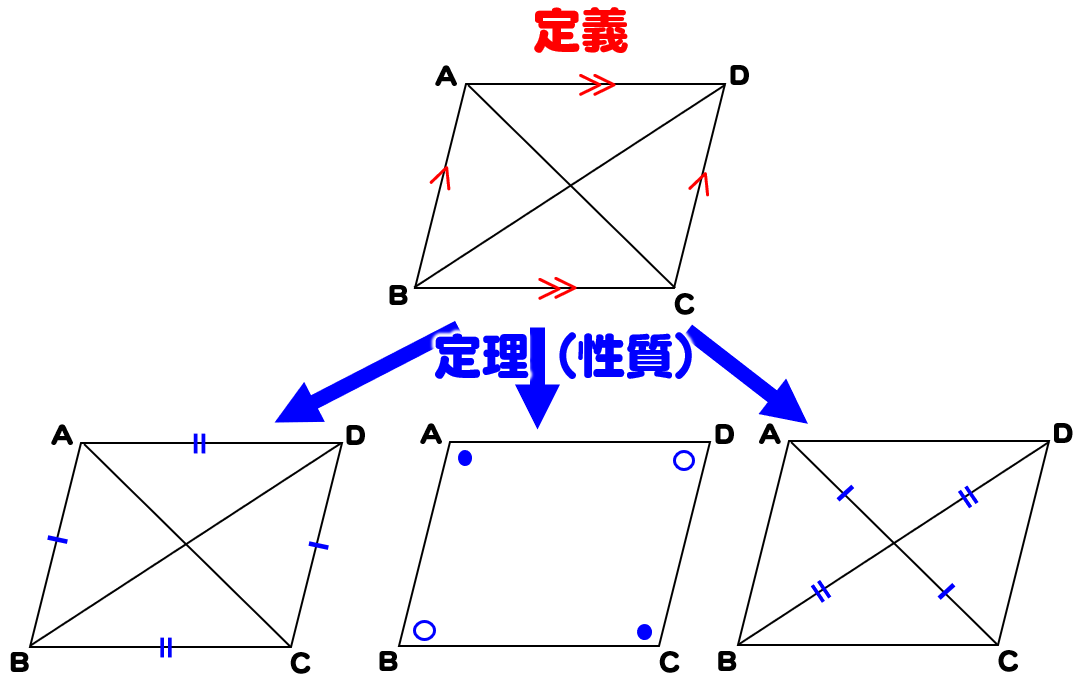
平行四辺形の対角線-長方形,正方形,台形,平行四辺形,ひし形の対角線の長さや交わり方について,次のア, イ,ウにあてはまるものを選び, を書きましょう。 長方形 正方形 台形 平行四辺形 ひし形 ア 2本の対角線の長平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図)1 平行四辺形の向かい合う辺は等しい。(証明) 2 平行四辺形の向かい合う角は等しい。(証明) 3 平行四辺形の対角線は、それぞれの中点で交わる。



中学数学 平行四辺形の証明問題を徹底解説 数スタ
平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦! それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基 平行四辺形の対角線の中点を通る直線は、どのように引いても、その平行四辺形の面積を2等分しますか? これって中学数学?高校数学? / 中学数学ですが、公立学校では詳しくやりません力の合成が平行四辺形の対角線なら、(剛体の)天秤としてつりあっていることを示す。 上図で、点Eに力χと力yを加える。ESとERを延長する。合力は平行四辺形の対角線。 まず、どこに天秤棒と支点を作ったらいいのか。 (1)支点はAにする。
平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。平行四辺形の対角線の錯視に関するメッツガー説の検討実験(浜口) すなわち,平行四辺形の左右 の斜辺が直立し,上下の辺と 直角をなすように(長方形に なるように)しようとすれば, 長対角線は圧し縮めるられる ことになるからである.逆に, 90平行四辺形 (へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ 平行 である 四角形 のことである。
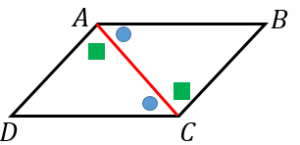
〔証明〕ひし形abcdの対角線ac,bdの交点をoとする。 aboと ( )において ひし形の定義から ( )=( ) ・・・1 ひし形は平行四辺形だから 対角線はそれぞれの中点で交わるから ( )=( ) ・・・2 また 平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 「 2本の対角線が垂直 ( 90° ) に交わる 」 と言う2つの条件が加われば、正方形になります。 正方形、長方形、ひし形はいずれも平行四辺形であり、平行四辺形の中でも、一定の条件を追加しS 長方形、三角形、二等辺三角形、直角三角形、四角すい T この図を見て、どんなことに気づきますか? S 合同な図形がある。錯角、対頂角がある。対角線の長さは等しい。4つの三角形の面積は等しい。



平行四辺形の証明 4 ネット塾




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
平行四辺形とは、2組の対辺が平行な四角形 (四辺形) のことである(※1)。 問題 平行四辺形が凸四角形であることを証明してください。 この問題に驚いたと思います。中高の数学では一度も出てきませんからね。でもここは『数学事始め』なのでこういうのもときどき出てきます。平行四辺形の続き 次に,長方形,ひし形,正方形の性質を扱いましょう. 定義 1.4つの角が等しい四角形を長方形という. 2.4辺の長さが等しい四角形をひし形という. 3.4つの角が等しくかつ4辺の長さの等しい四角形を正方形という. まず,長方形(2組の対角の大きさがそれぞれ等しい4 平行四辺形の性質を利用する証明問題 問題2 図のように,平行四辺形abcdの対角線ac上にae=cfとなるように,2点e,fをとる。このとき,be=dfであることを証明しなさい。 問題の見方 平行四辺形という条件から,次の3つの性質が活用できます。



余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会



Http Www News Ed Jp Gimu Yumeako Gakuryoku H26 H26cyusu H26cyusua 7 Pdf
命題1-43(平行四辺形の補形) 対角線をはさむ平行四辺形・補形 (作図対角線をはさむ平行四辺形) すべての平行四辺形において 対角線をはさむ 二つの平行四辺形の補形は 互いに等しい。 平行四辺形は、定義の補足(命題1-34)による。 対角線bdをひくところから証明していきましょう。 個別指導塾の基本問題に挑戦! 問題 下の図のような四角形abcdがあり、点e、f、g、hはそれぞれ各辺の中点であるとする。このとき、四角形efghが平行四辺形であることを、以下のように証明した。長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する




標準 平行四辺形とベクトルの演算 なかけんの数学ノート



高校入試 英語 数学 学習 三角形と四角形 平行四辺形
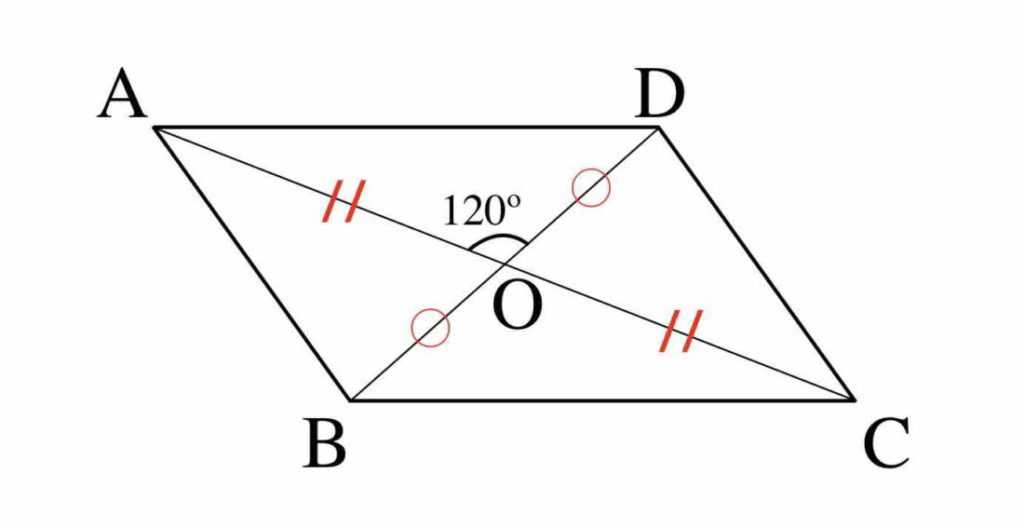
四角形は,1つの対角線で2つの三角形に分けることができます。 平行四辺形,ひし形,長方形,正方形は,1つの対角線で,形も 大きさも同じ2つの三角形に分けることができます。 trsA6F3tmpjtd 岩倉市日本語・ポルトガル語適応指導教室 平行四辺形 abcd と対角線の交点 o について考えます。 このとき、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ として、他のベクトルを $\vec{a}$, $\vec{b}$ で表してみましょう。∠a=∠cbe(平行線になる条件) AB//DC AD//BC <戻る> 4 対角線が、それぞれの中点で交わる。 ABOと CDOで AO=CO 1 BO=DO 2 対頂角)3 1,2,3より2辺とその間の角がそれぞれ等しいので




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
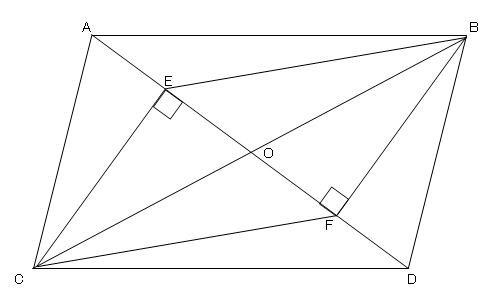
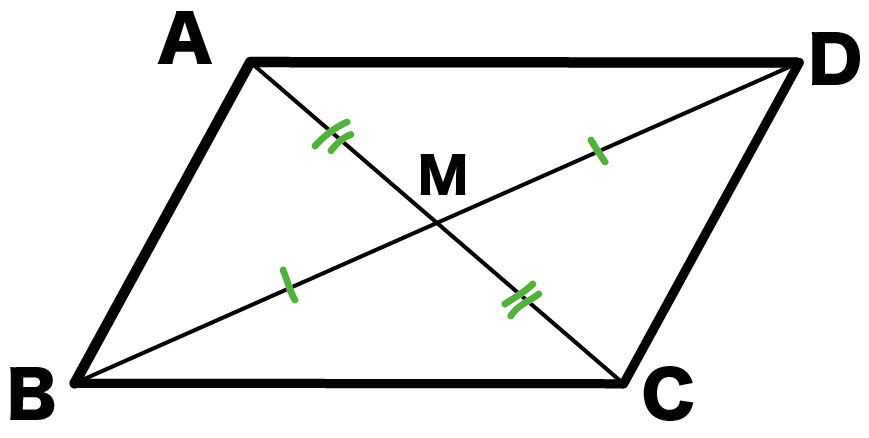
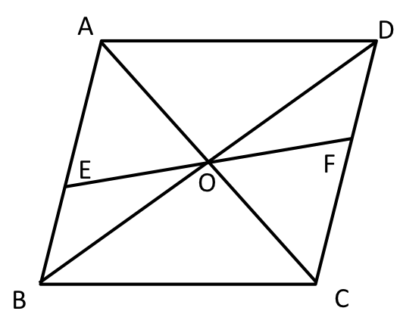
平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理(性質) 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう四角形を平行四辺形としよう」 と決めたことなのでAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators平行四辺形abcd対角線の交点oを通る直線をひき、ab, cdとの交点をそれぞれe、fとすると、 oe=ofとなることを証明しましょう。 aeoと cfoにおいて 平行四辺形では、対角線はそれぞれの中点で交わるのでao=co・・・① ?ので∠aoe=∠cof・・・② 正解 :対頂角は等しい



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生



フロー 2 5 5 2 平行四辺形の性質を利用した証明
平行四辺形の面積は dbcを2倍した値になるので24となります。 以上より rpqの面積を1としたとき、平行四辺形abcdの面積は24となるので 答えは24倍 となります。 ちょっと難しかったけど これも面積比を確実に見ていけば大丈夫な問題ですね! まとめ なぜ,平行四辺形は線対称の図形ではないのですか? 平行四辺形の右上を左下に折ると,ぴったり重ならないのですか? 教えてください。 進研ゼミからの回答 線対称な図形とは,1つの直線を折り目にして折ったとき平行四辺形の定義 (AB//CD, AD//CB)から、「対角線はそれぞれの中点で交わる」を証明する。 A B C D O




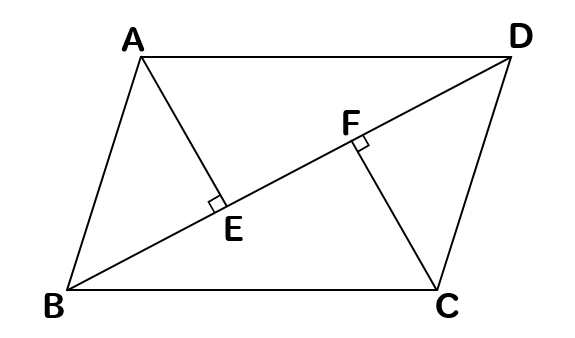
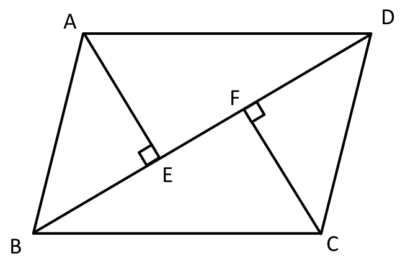
平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
平行四辺形とは 向かい合う2組の辺が それぞれ平行である四辺形をいう。 対角線とは向かい合う角を結ぶ線分をいう。 (以下、定義の補足(命題1ー34)(平行四辺形・対角線)という) 平行四辺形、対角線の用語は初めてここに登場する。 対辺、対角はテーマ7 平行四辺形の性質 2組の対辺がそれぞれ平行な四角形を平行四辺形という。(定義) 平行四辺形には,次の性質がある。 定理 1 2組の対辺はそれぞれ等しい。 2 2組の対角はそれぞれ等しい。 3 対角線はそれぞれの中点で交わる。ブリタニカ国際大百科事典 小項目事典 平行四辺形の用語解説 2組の対辺がともに平行である四角形。次のような性質をもつ。(1) 2組の対辺の長さはそれぞれ等しい。(2) 2組の対角の大きさはそれぞれ等しい。(3) 2本の対角線はそれぞれの中点で交わる。1組の対辺が平行な四角形は台形なので



1



平行四辺形の性質の証明




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




平行四辺形 Wikipedia



1




Math 平行四辺形 平行四辺形になることの証明 働きアリ




平行四辺形の対角線の交点の座標を求める はしもとの つれづれ




平行四辺形で知っておくべきこと 苦手な数学を簡単に




中学数学 平行四辺形の証明問題を徹底解説 数スタ




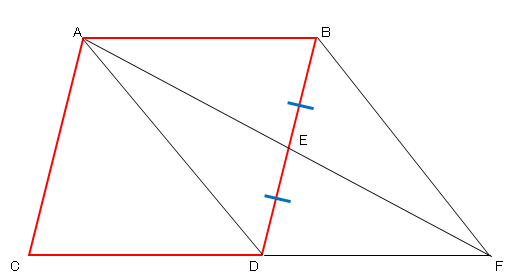
平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 中学校 教えて Goo




高校数学b ベクトルの成分表示と平行四辺形 受験の月



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ



1



平行四辺形の角の二等分線



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生



平行四辺形の性質




いまさら聞けない どうして速度の分解 合成は平行四辺形で考えるのか Koko物理 高校物理



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



平行四辺形の性質



平行四辺形の二つの対角線の長さが違う理由って何ですか Aklv721 Yahoo 知恵袋




平行四辺形の簡単な書き方 超数学館match 数学に特化した徹底個別指導塾 高崎 前橋




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室
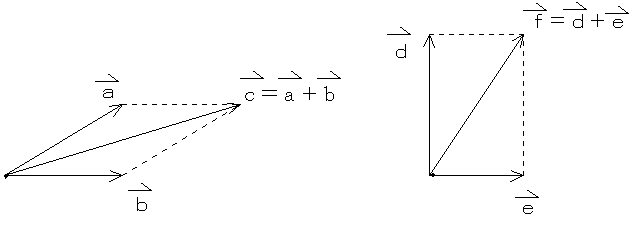



力の平行四辺形
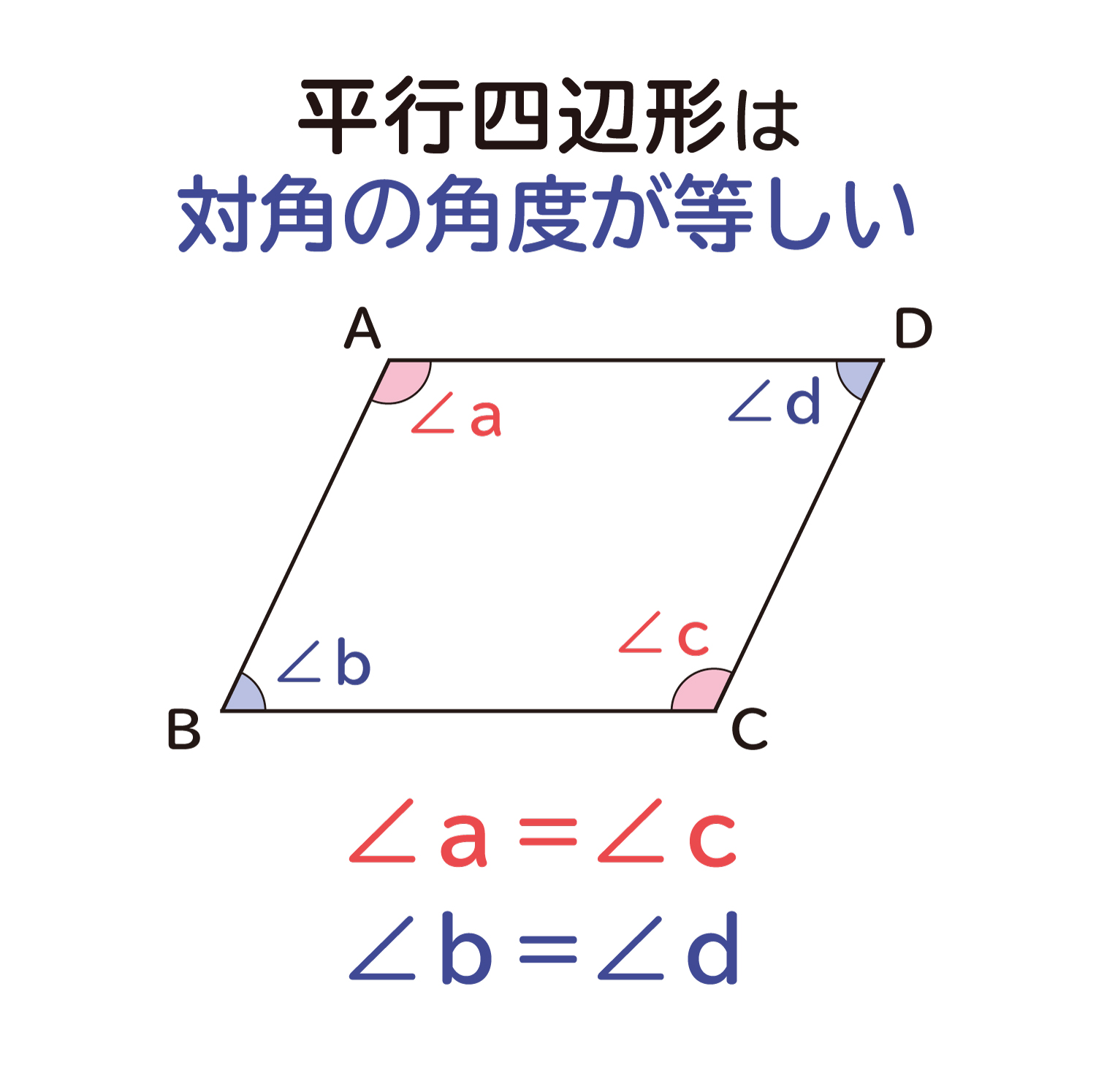



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




対角線と四角形 Youtube




合同な図形 内角 Ict教材eboard イーボード



平行四辺形の面積の2等分
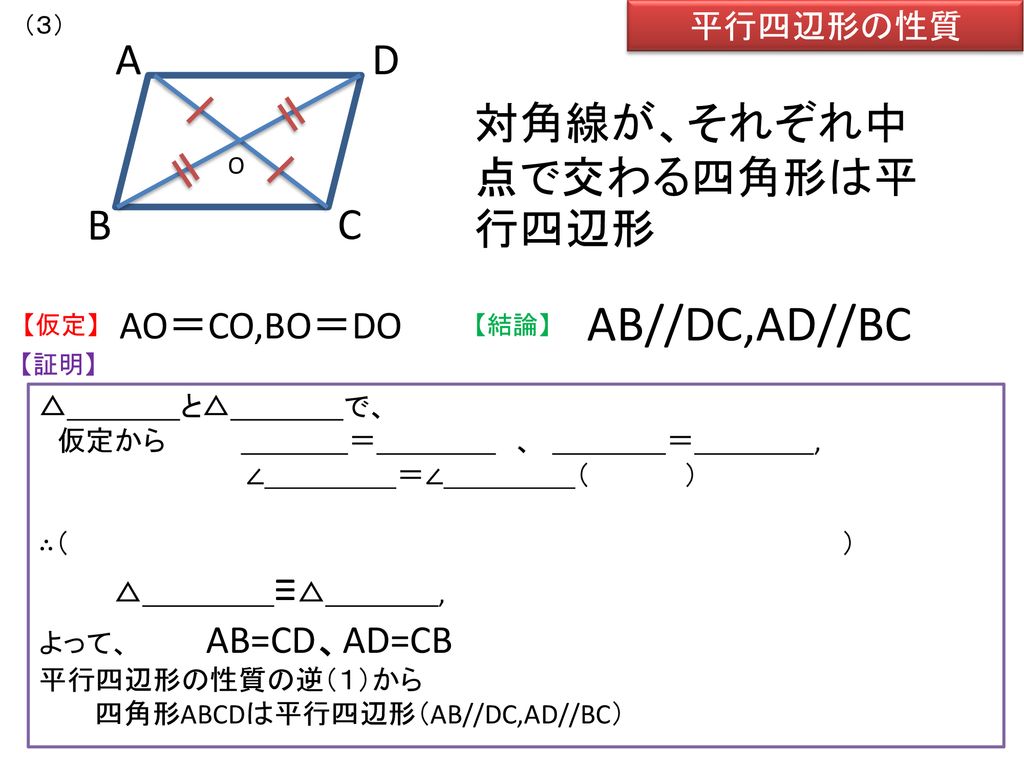



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




平行四辺形の面積を対角線と角度から求める問題 Youtube
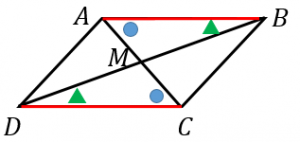



平行四辺形の3つの性質とその証明 具体例で学ぶ数学
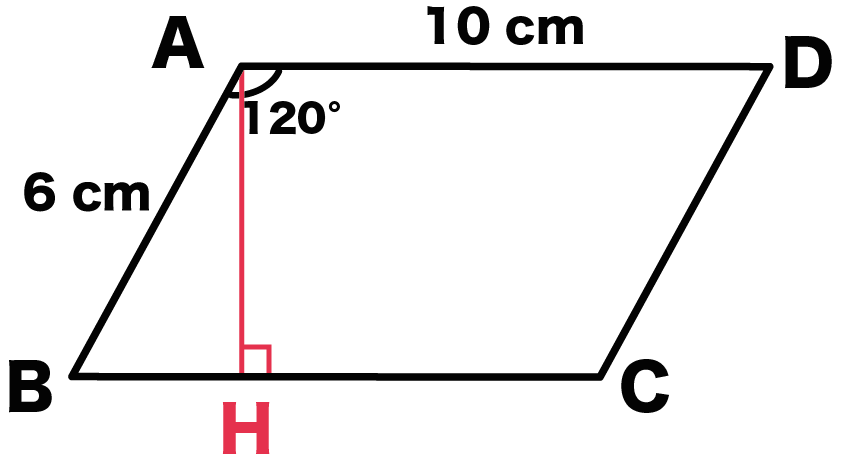



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



平面図形の基礎




平行四辺形の辺や角を求める Youtube



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



筑波大学附属駒場中学校2003年第1問 解答 解説




平行四辺形の対角線が他の対角線の中点を通ることの証明 うさぎめし C




相似 平行四辺形と面積比の問題を徹底解説 数スタ



ベクトルの問題です 平行四辺形oacbにおいて 対角線の Yahoo 知恵袋



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



5 図形と合同 2章 平行四辺形 1 平行四辺形 5時間 Ppt Download



三角比を用いた面積計算をマスターしよう スタディクラブ情報局



平行四辺形の対角線の角度について この条件の時の角度a Bを文字で表 Yahoo 知恵袋




平行四辺形の辺や角を求める Youtube




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




オイラー線の定理 Http Homepage2 Nifty Com Yoshio Oka Ma 人力検索はてな




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
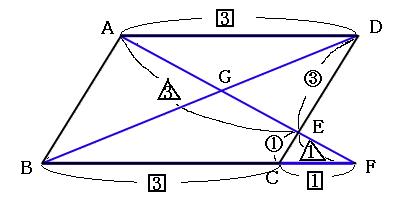



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ
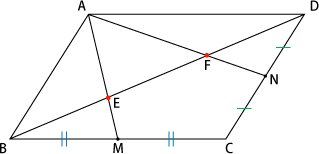



基礎学力アップシート 3年生 平行四辺形の辺の比を考えよう
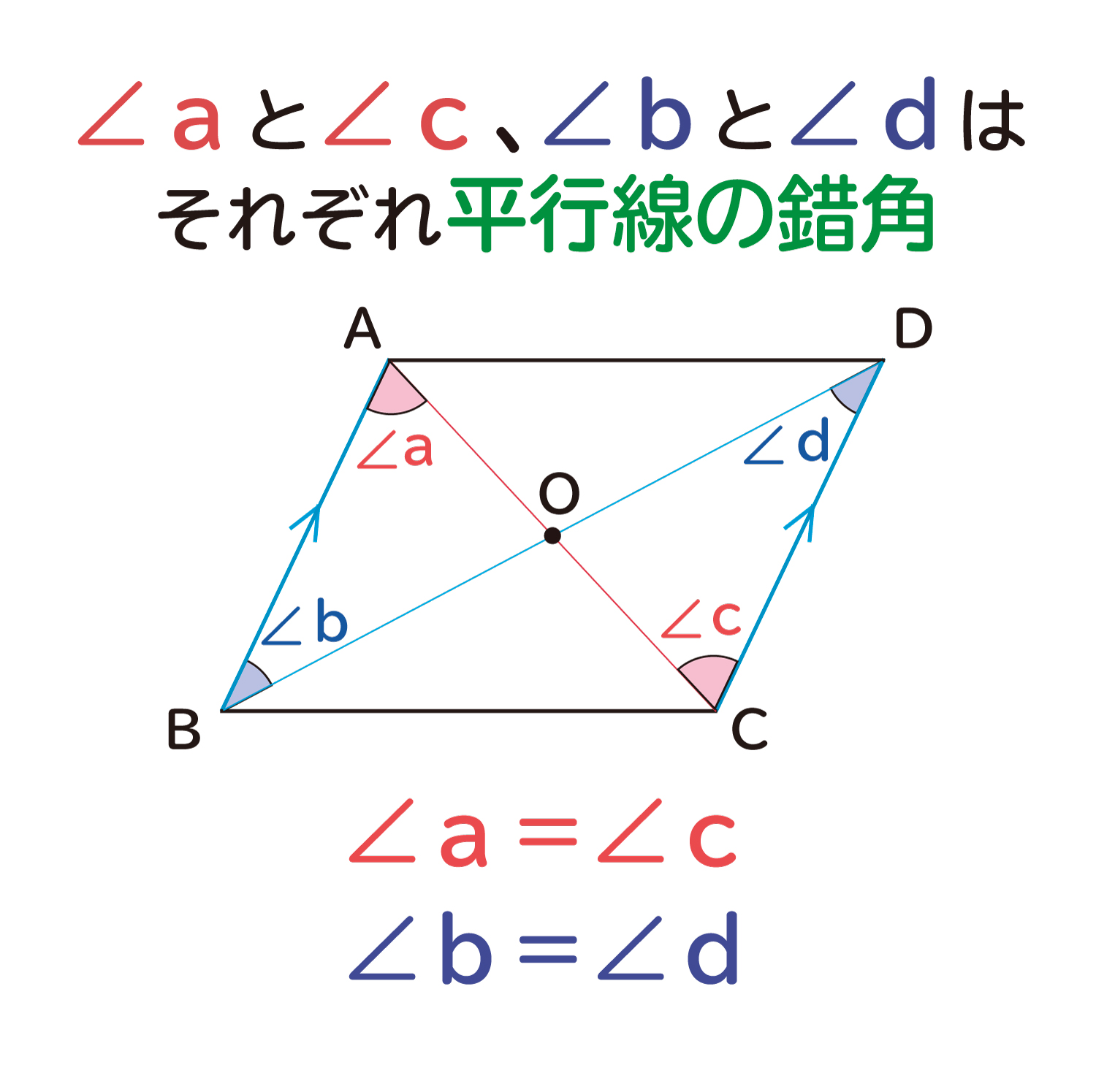



平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
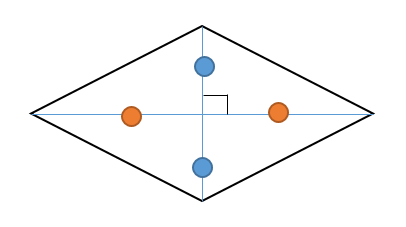



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
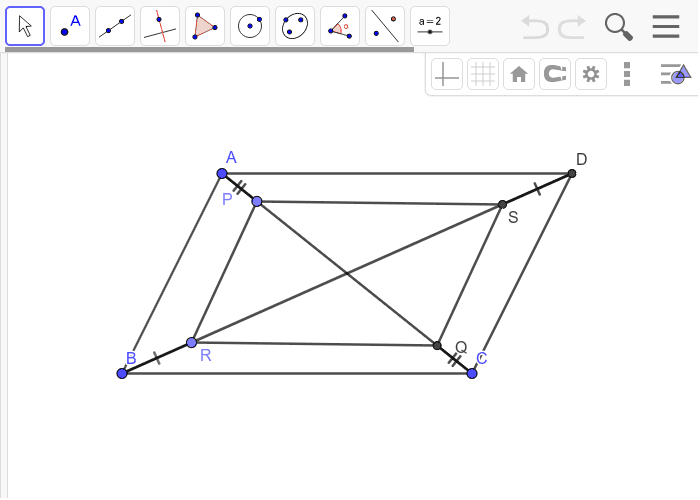



平行四辺形になるための条件 例 Geogebra
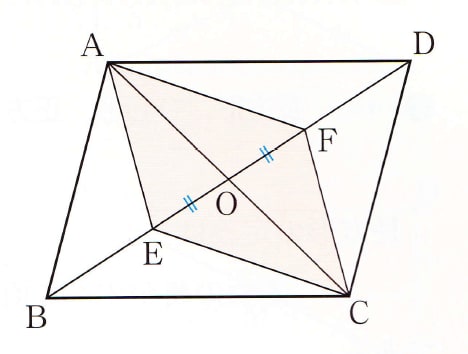



証明 は と が Takapの数学日記
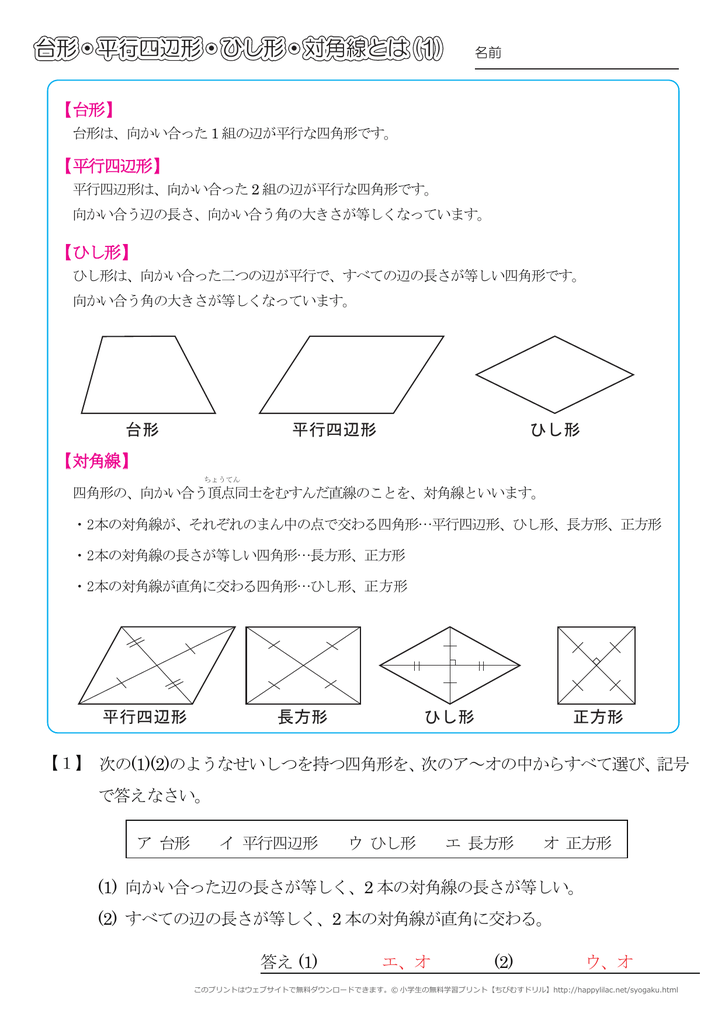



台形 平行四辺形 ひし形 対角線とは 1




証明分かりません 教えてください Clear
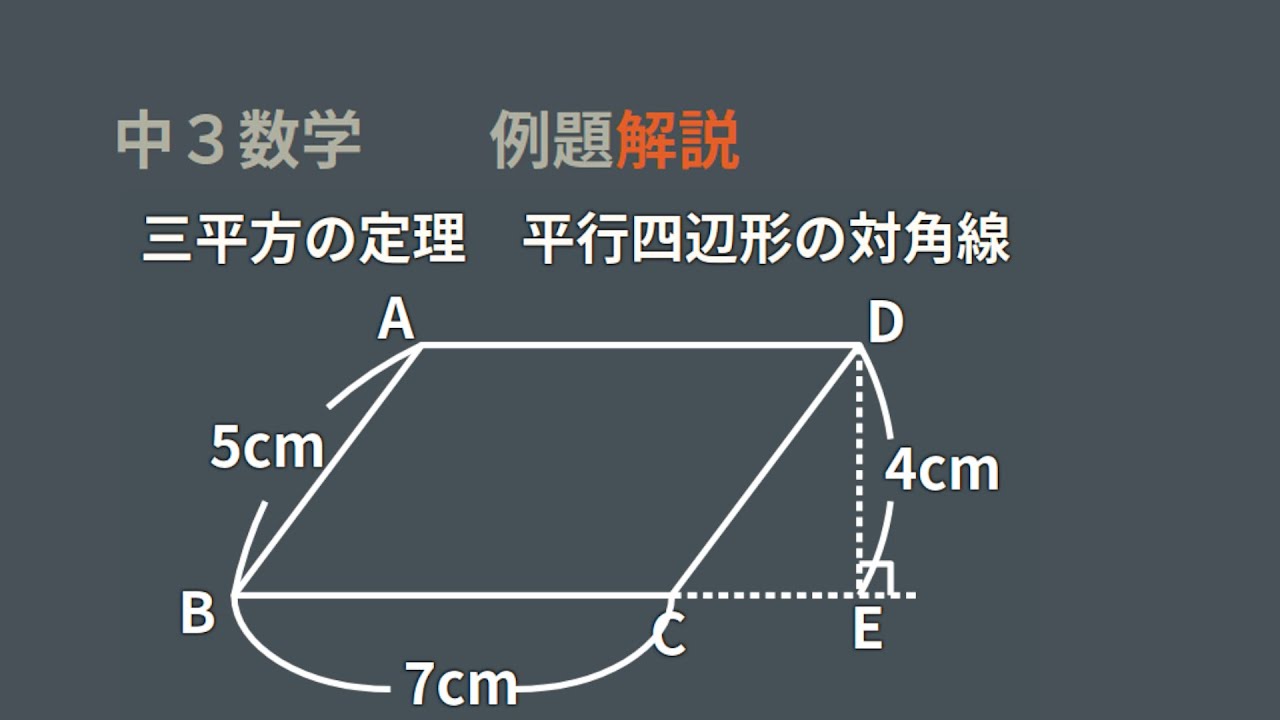



三平方の定理 平行四辺形の対角線



1




四角形 Ict教材eboard イーボード




平行四辺形の対角線の交点を頂点とする三角形の面積 Okwave
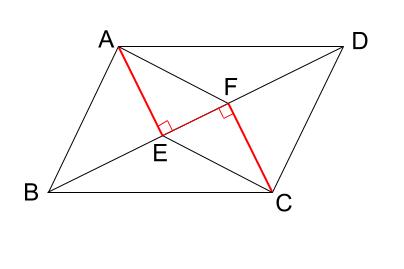



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su
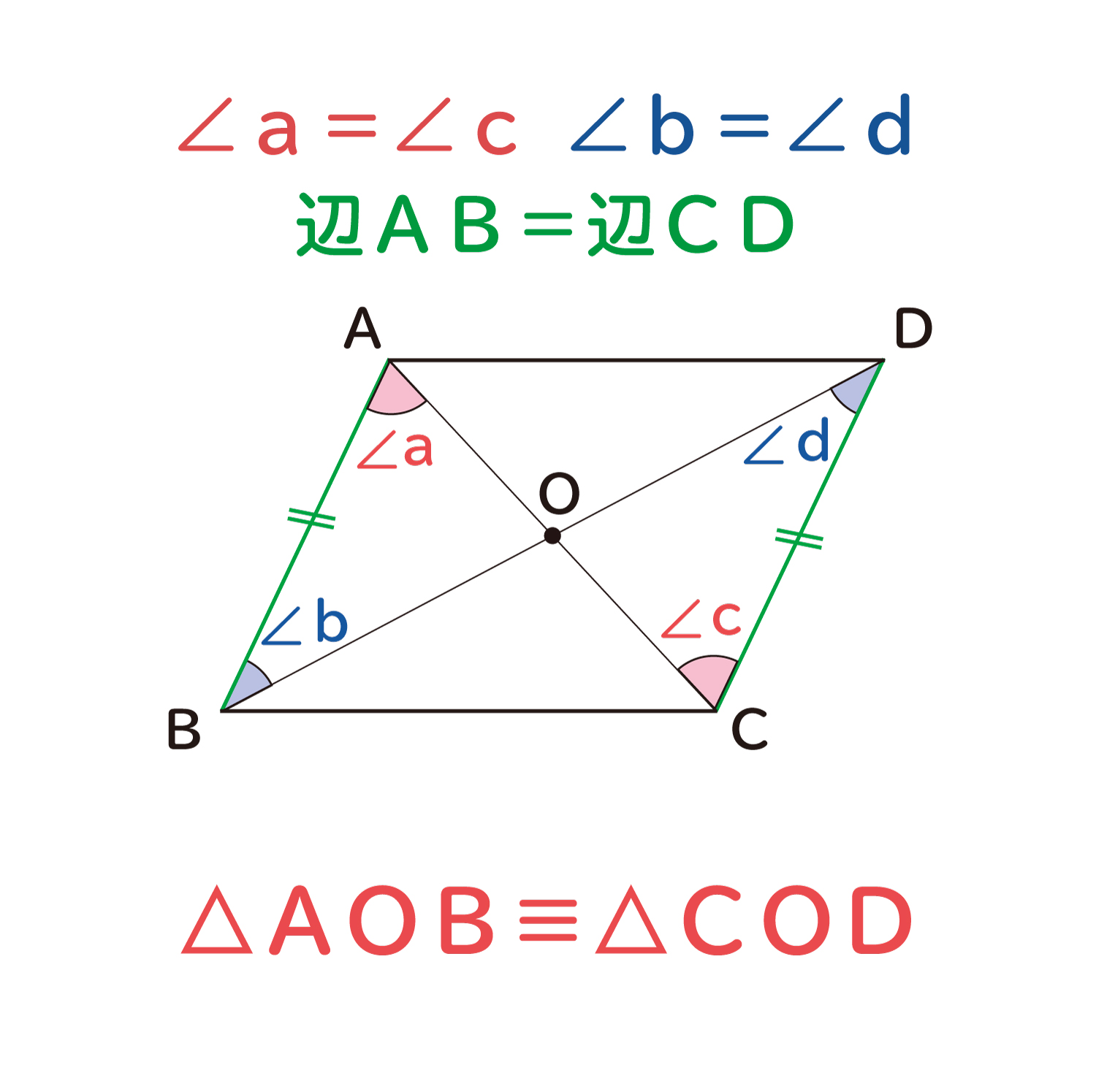



平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
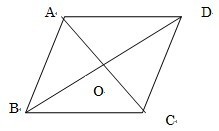



平行四辺形の性質の証明 平行四辺形の対角線は それぞれの中点で交わる 中学 無料問題 リンク集




平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear



フロー 2 5 5 2 平行四辺形の性質を利用した証明



平行四辺形の証明 2 ネット塾



平行四辺形と長方形 ひし形 正方形の関係 苦手な数学を簡単に



第175問の解答



今月の問題 平行四辺形



4年算数 垂直 平行と四角形 2 教え方



平行四辺形の性質の利用2




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




3 Abcd0 e Descubre Como Resolverlo En Qanda



平行四辺形の定義と性質 証明問題の解き方 数学fun



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



対角線で参観 教育考現学




Sqrt7 Abcd A D Descubre Como Resolverlo En Qanda




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




平行四辺形の対角線はそれぞれの中点で交わることの証明 をしないとい 中学校 教えて Goo




平行四辺形の対角線の長さの求め方




勉強しよう数学 余弦定理に類似した公式の多さの解決策はベクトル




定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校
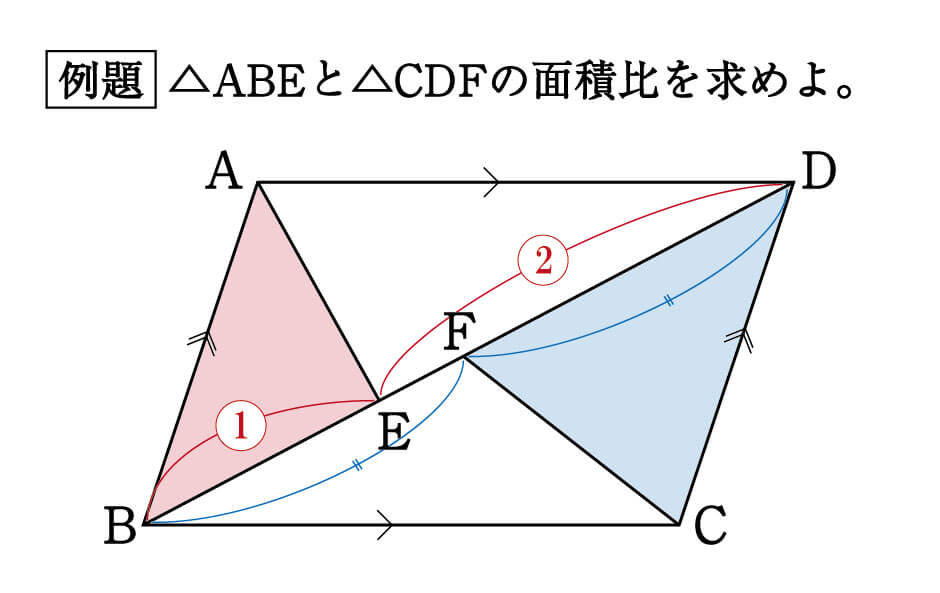



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
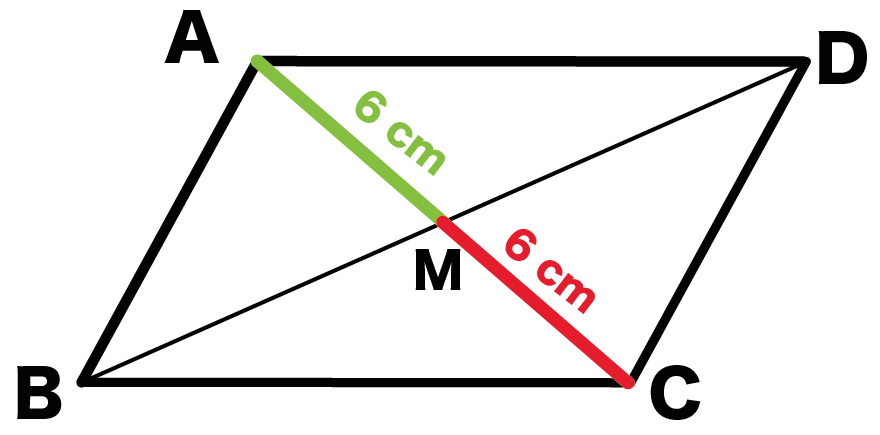



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿